boxplot(airquality$Ozone)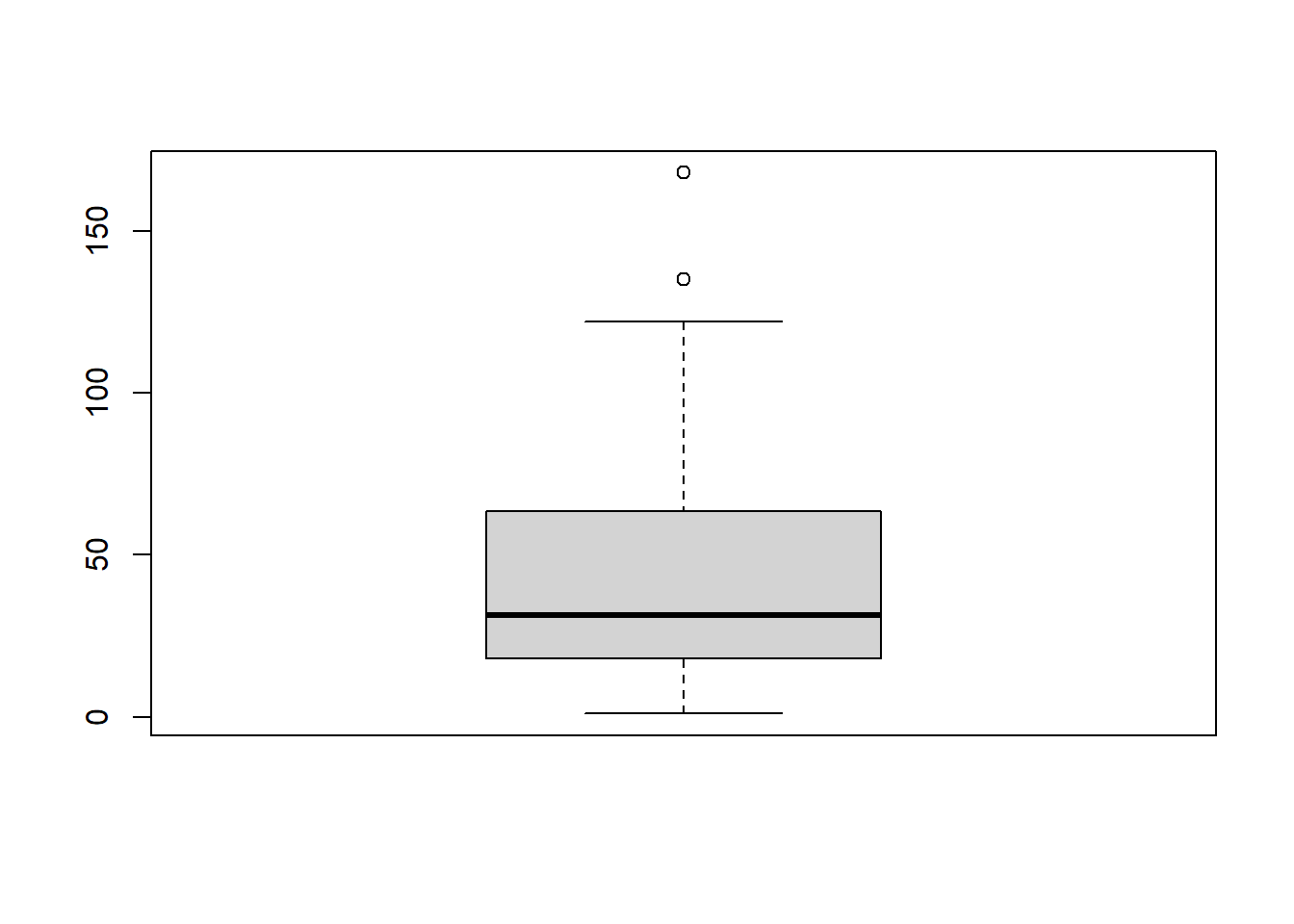
R in statistics
👉🏻Click to enter the ENV222 note section
1.
The distribution is shown in Figure @ref(fig:box).
boxplot(airquality$Ozone)
2.
rticles
3.
plot(1,
type = 'n',
axes = FALSE,
xlab = expression(NH[3] * " (" * mu* "mol m"^-3 * ")"),
ylab = '')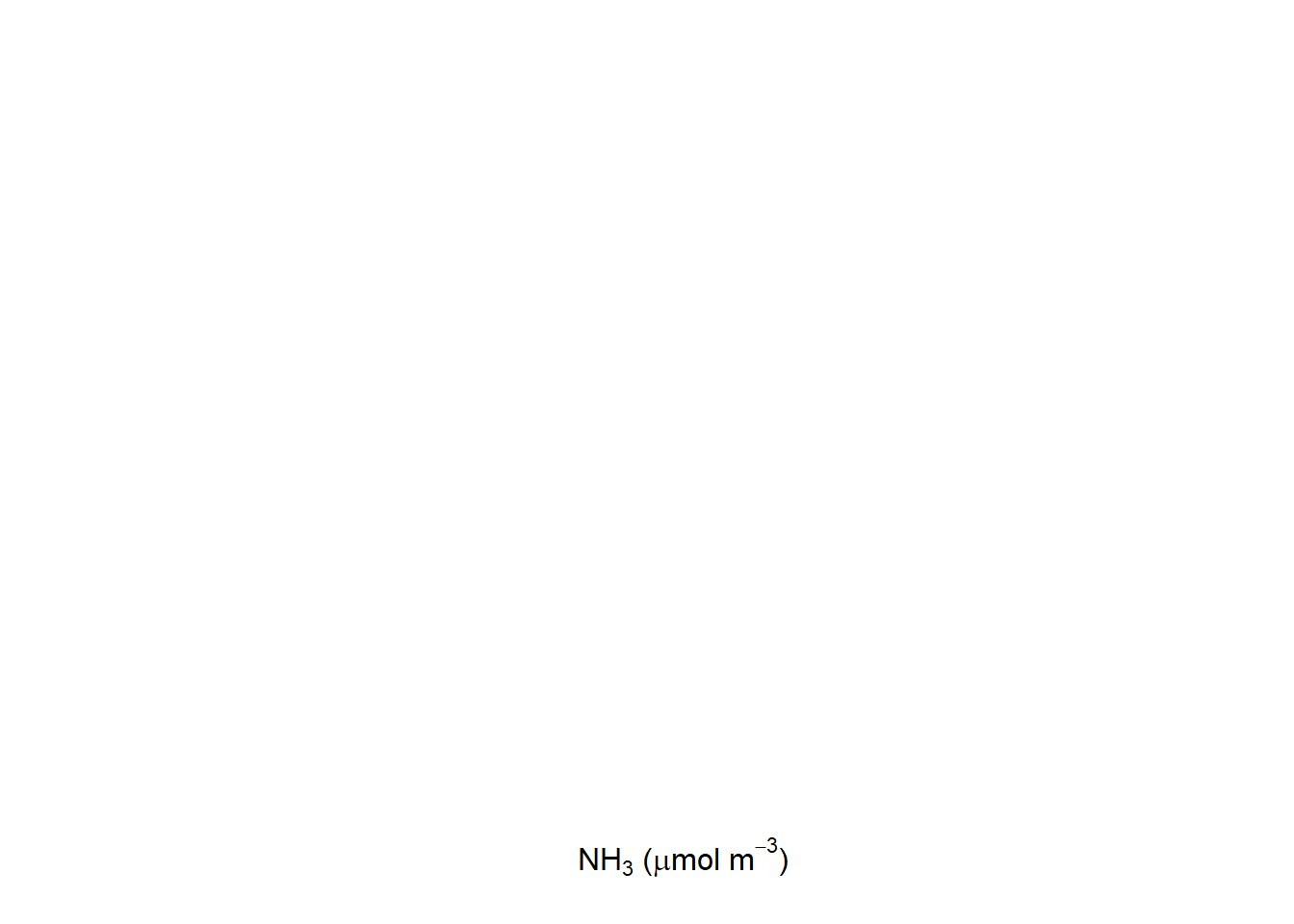
dtf <- c('1', '2', '3')
library(latex2exp)
plot(dtf, pch = 16, las = 1,
xlab = TeX('$NH_3$ ($\\mu$mol m$^{-3}$)'),
xaxt = "n", yaxt ="n",
line=0.4)
mymat <- matrix(c(1, 2, 3, 0), nrow = 2)
layout(mymat, widths = c(4, 1), heights = c(2, 1)) # Set the ratio between widths and heights
plot(iris$Sepal.Length, iris$Sepal.Width, pch=20, xlab='Sepal Length (cm)', ylab='Sepal Width (cm)', las=1)
boxplot(iris$Sepal.Length, pch=20, las=1, horizontal=T)
boxplot(iris$Sepal.Width, pch=20, las=2)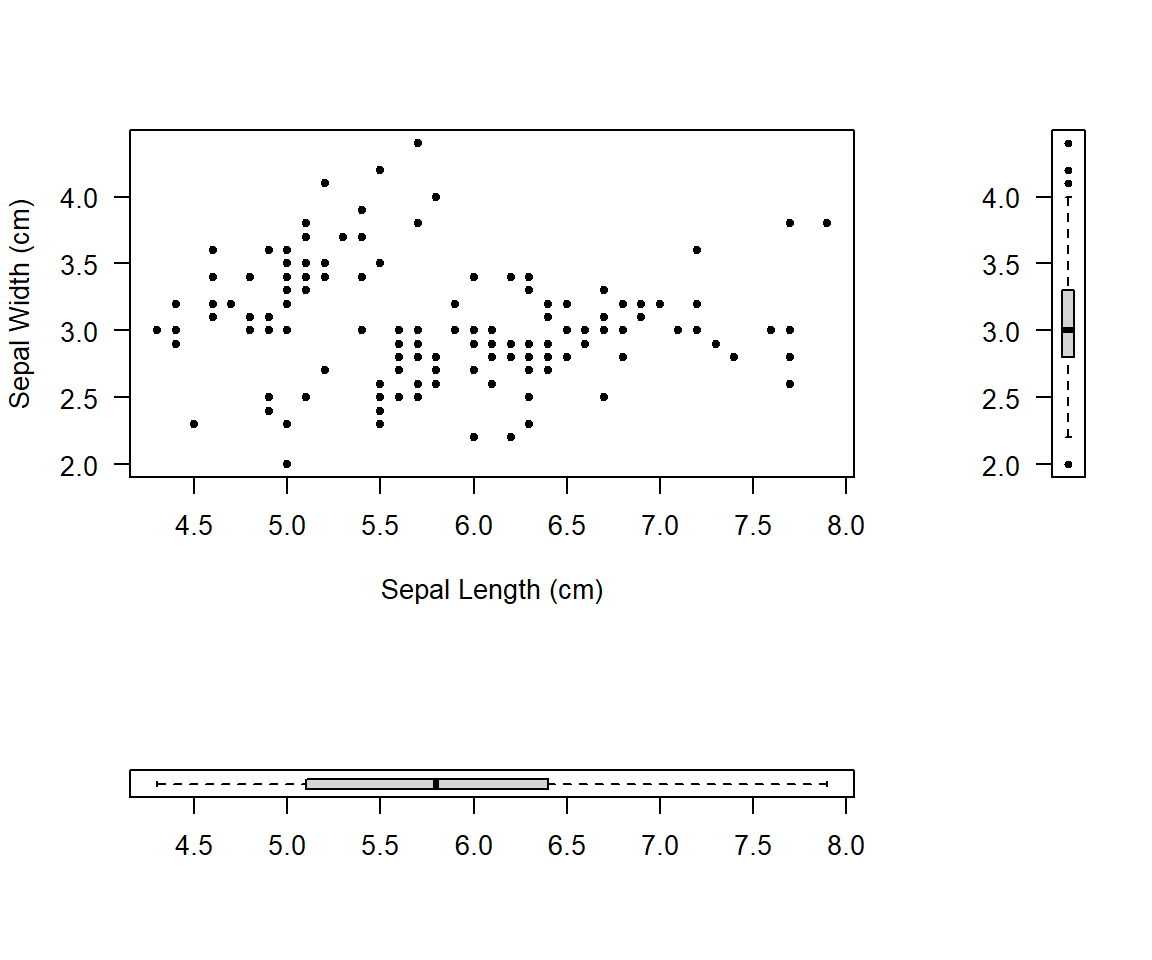
x <- 'pack my box with five dozen liquor jugs'
xsingle <- strsplit(x, split = "")[[1]]
xsingle <- xsingle[xsingle != " "]
length(xsingle)[1] 32mytab <- table(xsingle)
names(mytab[mytab == max(mytab)])[1] "i" "o"library(dplyr)
x <- "pack my box with five dozen liquor jugs"
char_freq <- gsub(" ", "", x) |>
strsplit("") |>
table() |>
data.frame() |>
arrange(desc(Freq))
head(char_freq, 5) Var1 Freq
1 i 3
2 o 3
3 e 2
4 u 2
5 a 1xword <- strsplit(x, " ")[[1]]
xword[which.max(nchar(xword))][1] "liquor"gsub('five', '5', x)[1] "pack my box with 5 dozen liquor jugs"[1] "English_United States.1252"sum(diff(mydata$date) != 1)[1] 0mydata$year <- as.integer(format(mydata$date, '%Y'))mydata$month <- format(mydata$date, '%B')mydata$weekday <- format(mydata$date, '%A')Result:
mydata# A tibble: 65,533 × 13
date ws wd nox no2 o3 pm10 so2 co pm25
<dttm> <dbl> <int> <int> <int> <int> <int> <dbl> <dbl> <int>
1 1998-01-01 00:00:00 0.6 280 285 39 1 29 4.72 3.37 NA
2 1998-01-01 01:00:00 2.16 230 NA NA NA 37 NA NA NA
3 1998-01-01 02:00:00 2.76 190 NA NA 3 34 6.83 9.60 NA
4 1998-01-01 03:00:00 2.16 170 493 52 3 35 7.66 10.2 NA
5 1998-01-01 04:00:00 2.4 180 468 78 2 34 8.07 8.91 NA
6 1998-01-01 05:00:00 3 190 264 42 0 16 5.50 3.05 NA
7 1998-01-01 06:00:00 3 140 171 38 0 11 4.23 2.26 NA
8 1998-01-01 07:00:00 3 170 195 51 0 12 3.88 2.00 NA
9 1998-01-01 08:00:00 3.36 170 137 42 1 12 3.35 1.46 NA
10 1998-01-01 09:00:00 3.96 170 113 39 2 12 2.92 1.20 NA
# ℹ 65,523 more rows
# ℹ 3 more variables: year <int>, month <chr>, weekday <chr>1.
C
2.
B
3.
Wilcoxon Rank-Sum test
4.
5.
There are no duplicated values, because the rank are all int
rank(c(13.31, 13.67, 12.805, 13.1, 13.39, 12.375, 11.58, 14.58, 12.029, 13.69)) [1] 6 8 4 5 7 3 1 10 2 9rank(c(14.14, 12.54, 15.63, 13.66, 15.51, 13.23, 13.25, 15.2, 14.18, 14.53)) [1] 5 1 10 4 9 2 3 8 6 76.
Test statistic value: W = 23
dtf <- data.frame(City_A = c(13.31, 13.67, 12.805, 13.1, 13.39, 12.375, 11.58, 14.58, 12.029, 13.69),
City_B = c(14.14, 12.54, 15.63, 13.66, 15.51, 13.23, 13.25, 15.2, 14.18, 14.53))
test <- wilcox.test(dtf$City_A, dtf$City_B, conf.int=TRUE)
test$statistic W
23 7.
Critical values of 95 percent confidence interval: 24, 76
dtf <- data.frame(conc = c(13.31, 13.67, 12.805, 13.1, 13.39, 12.375, 11.58, 14.58, 12.029, 13.69, 14.14, 12.54, 15.63, 13.66, 15.51, 13.23, 13.25, 15.2, 14.18, 14.53),
city = c(rep("A", 10), rep("B", 10)))
m <- sum(dtf$city == "A")
n <- sum(dtf$city == "B")
U_critical <- qwilcox(c(0.025, 0.975), m, n)
U_critical[1] 24 76dtf <- data.frame(City_A = c(13.31, 13.67, 12.805, 13.1, 13.39, 12.375, 11.58, 14.58, 12.029, 13.69),
City_B = c(14.14, 12.54, 15.63, 13.66, 15.51, 13.23, 13.25, 15.2, 14.18, 14.53))
m <- nrow(dtf)
n <- nrow(dtf)
U_critical <- qwilcox(c(0.025, 0.975), m, n)
U_critical[1] 24 76U <- 23
m <- 10
n <- 10
curve(dwilcox(x, m, n), from = 0, to = 100, n = 101, ylab = 'Probability distribution density', las = 1, type = 'S', ylim = c(0, 0.031))
abline(h = 0)
segments(x0 = c(U, U_critical), y0 = 0, x1 = c(U, U_critical), y1 = dwilcox(c(U, U_critical), m, n), col = c('blue', 'red', 'red'))
legend('topright', legend = c('Distribution curve', 'Critical values', 'U score'), col = c('black', 'red', 'blue'), lty = 1,cex=0.7)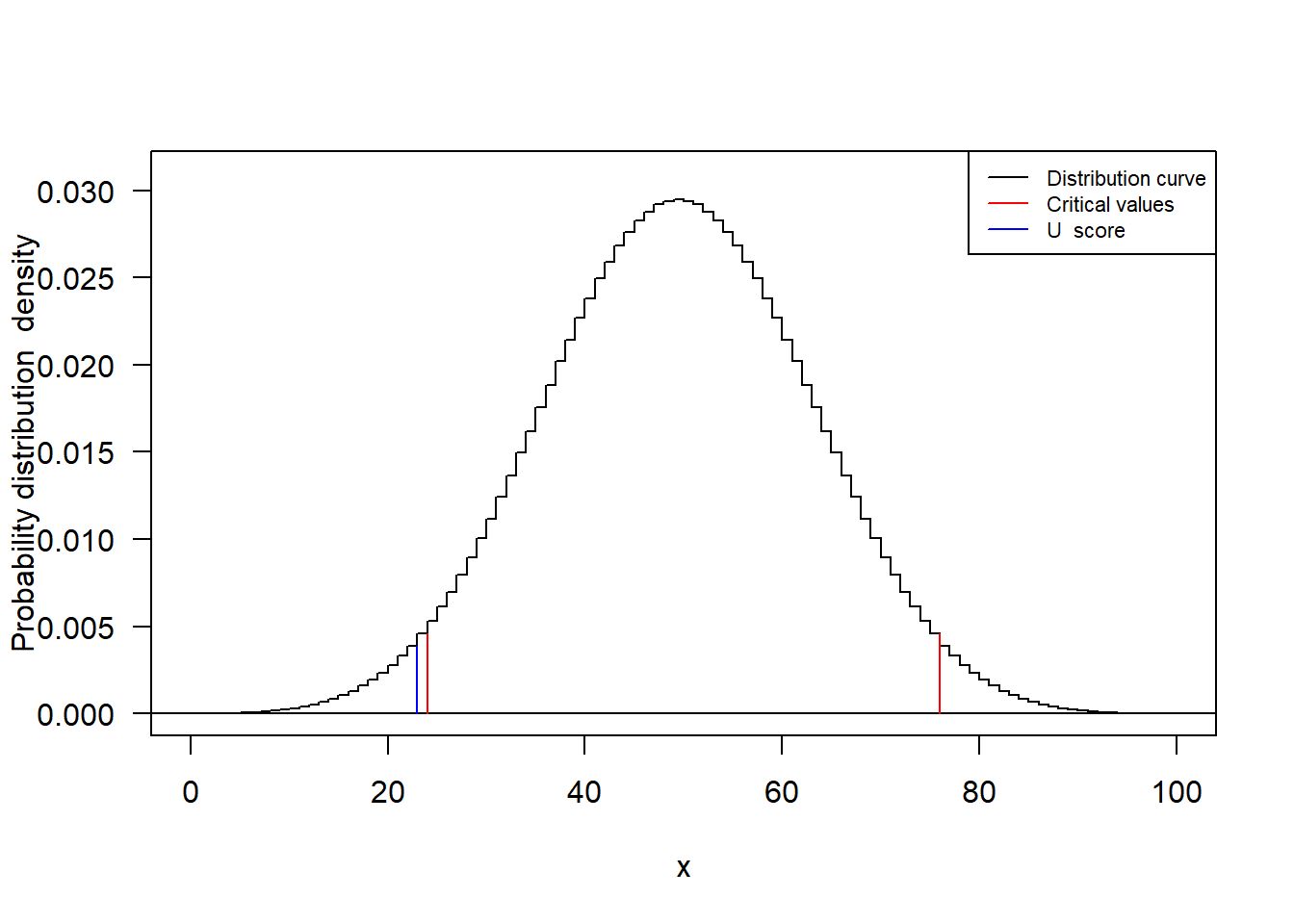
9.
The P-value is 0.043
dtf <- data.frame(City_A = c(13.31, 13.67, 12.805, 13.1, 13.39, 12.375, 11.58, 14.58, 12.029, 13.69),
City_B = c(14.14, 12.54, 15.63, 13.66, 15.51, 13.23, 13.25, 15.2, 14.18, 14.53))
test <- wilcox.test(dtf$City_A, dtf$City_B, conf.int=TRUE)
round(test$p.value, 3)[1] 0.04310.
The P-value is smaller than 0.05, reject the H0 hypotheses.
11.
The two dataset medians are different at alpha=0.05. The City_A and City_B have significant different with the median PM2.5 concentrations.
12.
The mean and standard deviation of the approximate normal distribution are 50 and 13.22876
U_mu <- m * n / 2
U_mu[1] 50U_sd <- sqrt(m * n * (m + n + 1) / 12)
U_sd[1] 13.2287613.
curve(dnorm(x, U_mu, U_sd), from=0, to=110)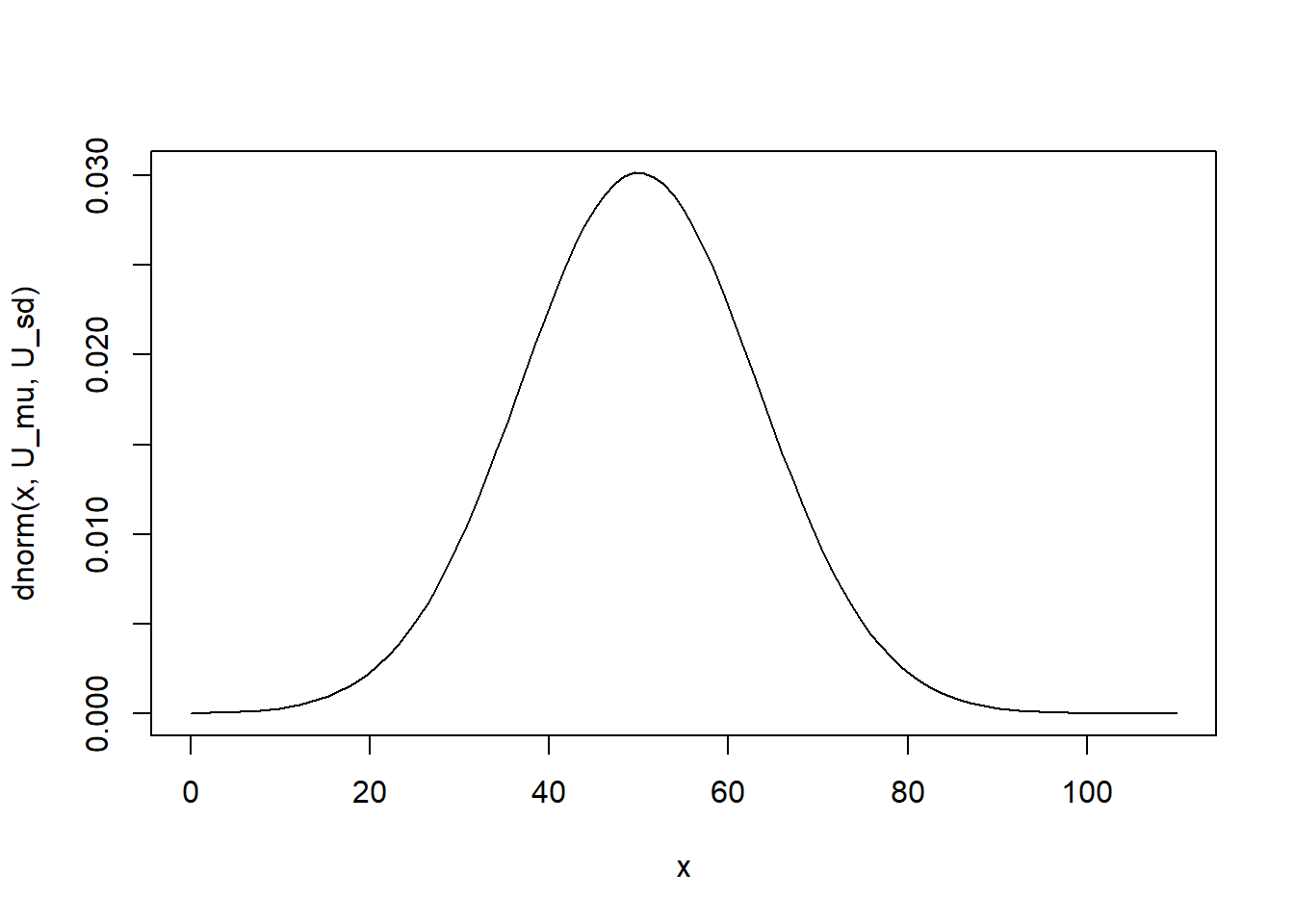
NA
NA
Sys.time()[1] "2023-05-11 12:27:12 CST"format(Sys.Date(), format = '%Y, %B, %d, %A')[1] "2023, May, 11, Thursday"t1 <- Sys.time()
t2 <- strptime( "2022-9-13 15:00:00", format="%Y-%m-%d %H:%M:%S" )
difftime(time1 = t1, time2 = t2, units = 'secs')Time difference of 20726833 secsdifftime(time1 = t1, time2 = t2, units = 'days')Time difference of 239.8939 daysdifftime(time1 = t1, time2 = t2, units = 'hours')Time difference of 5757.454 hourst3 <- as.Date( "9/13/2023", format="%m/%d/%Y" )
format(t3, format="%A")[1] "Wednesday"t4 <- as.Date( "9/13/2024", format="%m/%d/%Y" )
format(t4, format="%A")[1] "Friday"dates <- seq(as.Date("2020-09-13"), as.Date("2040-09-13"), by="year")
weekdays <- factor(weekdays(dates, abbreviate=TRUE),
levels=c("Sun", "Mon", "Tue", "Wed", "Thu", "Fri", "Sat"))
weekdays <- as.integer(format(dates, "%u"))
plot(weekdays, as.Date(dates, format="%Y" ),
xlab="Weekday", ylab="Year", main="September 13th, 2020-2040")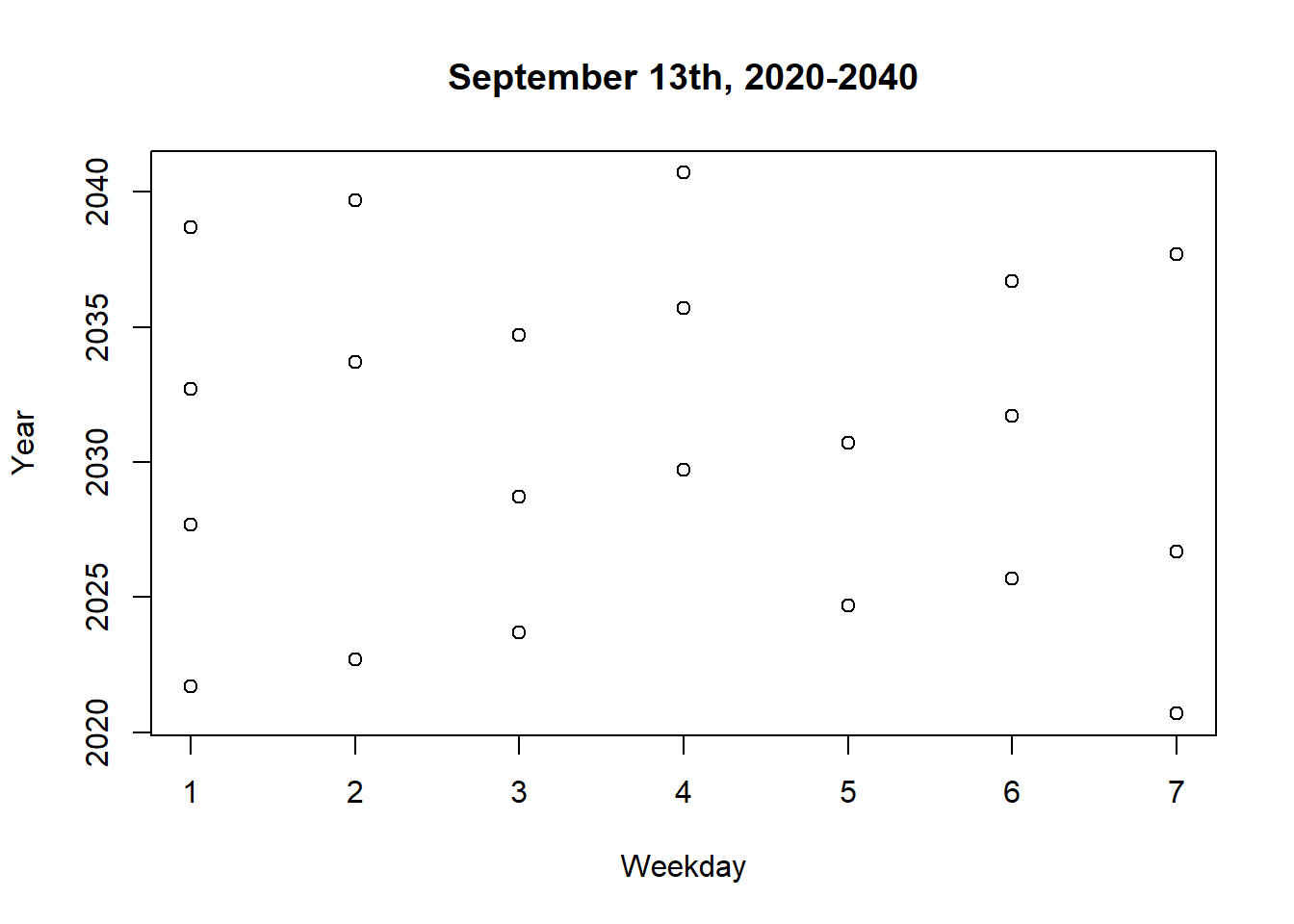
air<-read.csv("data/airquality.csv")
day <- paste("2022-",air$Month,"-",air$Day,sep="")
air$Date <- as.Date(day, format="%Y-%m-%d")air1<-na.omit(air)
subsets <- split(air1, air1$Month)
plots <- lapply(subsets, function(subset) {
plot(subset$Day, subset$Ozone,ylab = "Ozone pbb" ,main = paste("Ozone, ", unique(subset$Month))
)})
par(mfrow = c(2, 3))
for (i in seq_along(plots)) {
plot(plots[[i]])
}
library(ggthemes)
library(latex2exp)
dtf <- airquality
dtf5 <- dtf %>% subset(Date < "1973-06-01")
ggplot(dtf5) +
geom_point(aes(x = Date, y = Ozone))+
labs(y = "Ozone (ppb)") +
theme_classic() +
theme(axis.text.x = element_text(angle = 45, hjust = 1))
ggplot(dtf5) +
geom_point(aes(x = Date, y = Solar.R))+
labs(y = TeX("$\\text{Solar Radiation } (W\\cdot m^{-2})$")) +
theme_classic() +
theme(axis.text.x = element_text(angle = 45, hjust = 1))
ggplot(dtf5) +
geom_point(aes(x = Date, y = Wind))+
labs(y = TeX("$\\text{Wind speed }m\\cdot m^{-1}$")) +
theme_classic() +
theme(axis.text.x = element_text(angle = 45, hjust = 1))
ggplot(dtf5) +
geom_point(aes(x = Date, y = Temp))+
labs(y = TeX("$\\text{Temperature }\\circ C$")) +
theme_classic() +
theme(axis.text.x = element_text(angle = 45, hjust = 1))# install.packages("lubridate")
library(lubridate)
dtf$Weekday <- wday(as.Date(dtf$Date), week_start = 1)air1<-na.omit(air)
tapply(as.numeric(air1$Ozone),air1$Weekday,mean)
library(tidyverse)
mean_dtf <- dtf %>%
drop_na() %>%
group_by(Weekday) %>%
summarise(Ozone = mean(Ozone),
Solar.R = mean(Solar.R),
Wind = mean(Wind),
Temp = mean(Temp))library(latex2exp)
library(patchwork)
mean_ozone <- ggplot(mean_dtf) +
geom_line(aes(x = Weekday, y = Ozone)) +
labs(y = "Ozone (ppb)") +
theme_classic()
mean_solar <- ggplot(mean_dtf) +
geom_line(aes(x = Weekday, y = Solar.R)) +
labs(y = TeX("$\\text{Solar Radiation } (W\\cdot m^{-2})$")) +
theme_classic()
mean_wind <- ggplot(mean_dtf) +
geom_line(aes(x = Weekday, y = Wind))+
labs(y = TeX("$\\text{Wind speed }m\\cdot m^{-1}$")) +
theme_classic()
mean_temp <- ggplot(mean_dtf) +
geom_line(aes(x = Weekday, y = Temp))+
labs(y = TeX("$\\text{Temperature }\\circ C$")) +
theme_classic()setwd("data/smartflux/") # Remeber to delete the first file
temp <- list.files() %>%
substr(start = 1, stop =10) %>%
strptime(format = "%Y-%m-%d") %>%
format("%Y-%m-%d")
missing_files <- 0
for(i in 1:(length(temp)-1)){
diff <- as.vector(difftime(temp[i+1], temp[i], units = "days"))
if(diff != 1){
missing_files <- missing_files + diff -1
}
}
print(missing_files)
temp <- list.files()
files <- lapply(temp, function(i){
read.table(i, fill = TRUE)
})
missing_records <- 0
for(i in 1:length(files)){
records <- length(files[[i]][3:nrow(files[[i]]),4])
missing_records <- missing_records + 48 - records
}
missing_records <- missing_records + 48 * missing_files
print(missing_records)
library(latex2exp)
plot(iris$Sepal.Length, iris$Petal.Length, pch = 16, las = 1,
xlab = TeX('D$_p$($\\mu$m)'),
ylab = expression(frac('dN', 'dlogD'[p] * '(cm' ^-3 * ')')))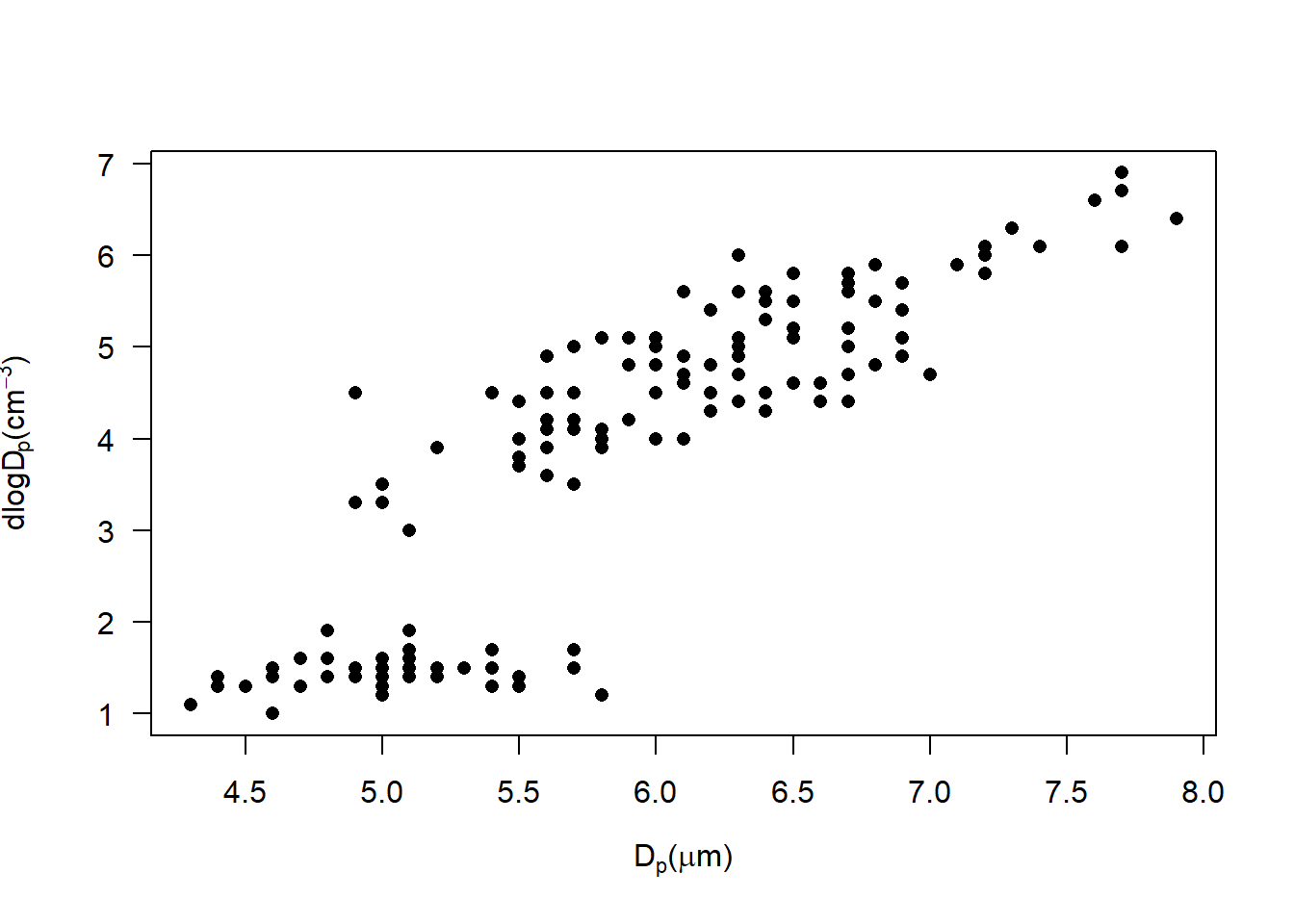
mymat <- matrix(c(1, 2, 3, 4), nrow = 2)
layout(mymat, widths = c(1, 2, 3, 2), heights = c(2, 1, 1, 2))
plot(co2)
plot(co2)
plot(co2)
plot(co2)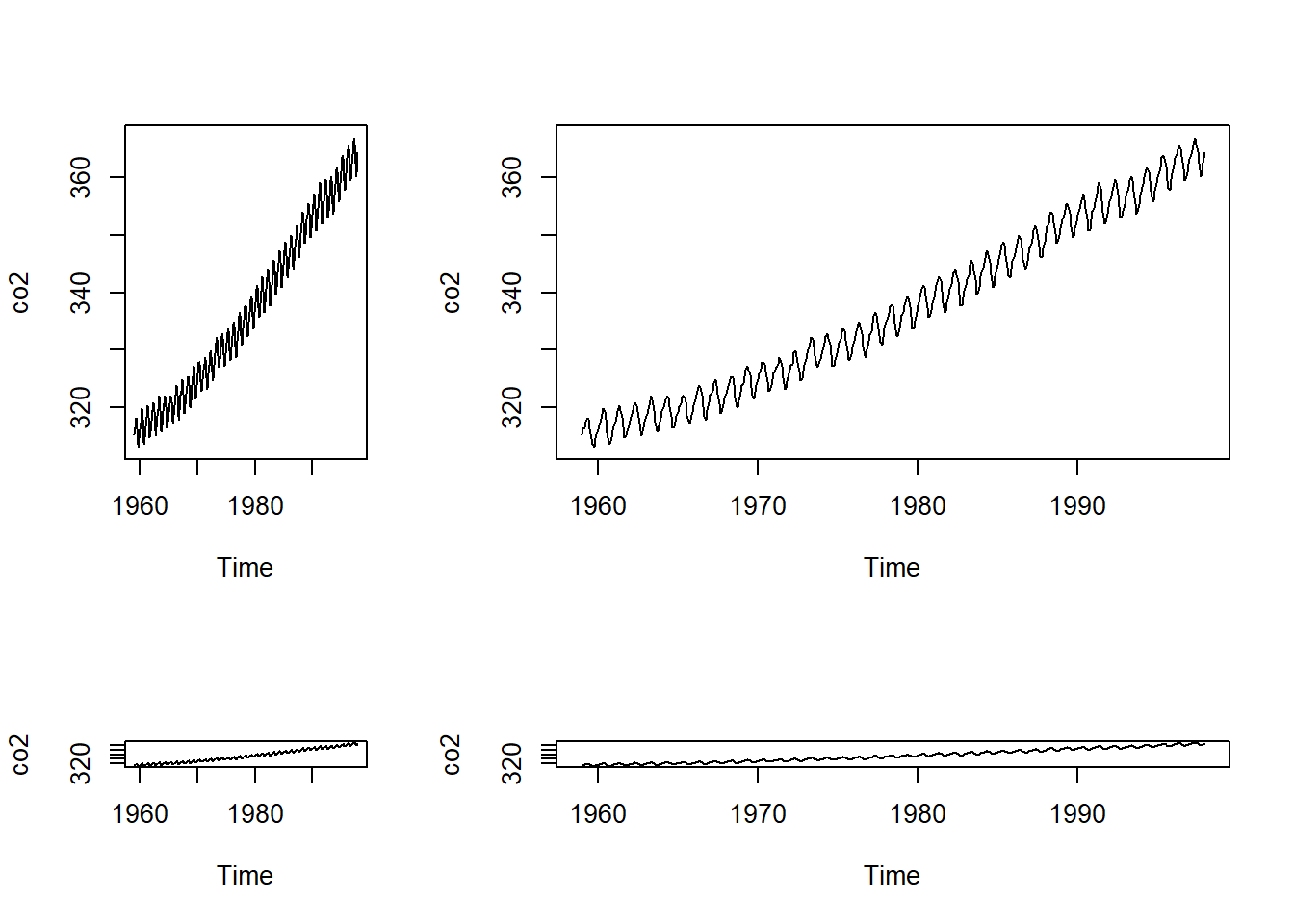
stocks <- data.frame(year = c(2015, 2015, 2016, 2016),
half = c( 1, 2, 1, 2),
return = c(1.88, 0.59, 0.92, 0.17))
stocks_wide <- stocks %>%
pivot_wider(names_from = half, values_from = return)
stocks_wide# A tibble: 2 × 3
year `1` `2`
<dbl> <dbl> <dbl>
1 2015 1.88 0.59
2 2016 0.92 0.17# because the column names 1999 and 2000 are not being correctly referenced.
table4a %>%
pivot_longer(c(`1999`, `2000`), names_to = "year", values_to = "cases")# A tibble: 6 × 3
country year cases
<chr> <chr> <dbl>
1 Afghanistan 1999 745
2 Afghanistan 2000 2666
3 Brazil 1999 37737
4 Brazil 2000 80488
5 China 1999 212258
6 China 2000 213766# Because there are duplicate values(columns) in the name and names columns (Not tidy)
people <- tribble(
~name, ~names, ~values,
"Phillip Woods", "age", 45,
"Phillip Woods", "height", 186,
"Phillip Woods", "age", 50,
"Jessica Cordero", "age", 37,
"Jessica Cordero", "height", 156
)preg <- tribble(
~pregnant, ~male, ~female,
"yes", NA, 10,
"no", 20, 12
)
preg1 <- pivot_longer(preg,c("male","female"),names_to = "Gender",values_to = "Number")
preg1# A tibble: 4 × 3
pregnant Gender Number
<chr> <chr> <dbl>
1 yes male NA
2 yes female 10
3 no male 20
4 no female 125.
(1) To determine which plane (tailnum) has the worst on-time record, we can calculate the average departure delay for each plane and then sort the results in ascending order to find the plane with the highest average delay.
# install.packages("nycflights13")
library(dplyr)
library(nycflights13)
flights %>%
group_by(tailnum) %>%
summarize(avg_dep_delay = mean(dep_delay, na.rm = TRUE)) %>%
arrange(desc(avg_dep_delay)) %>%
head(1)# A tibble: 1 × 2
tailnum avg_dep_delay
<chr> <dbl>
1 N844MH 297
(2) We should depart at 5am, with a smallest time of dalay of 0.688 min on average.
flights %>%
group_by(hour) %>%
summarize(avg_dep_delay = mean(dep_delay, na.rm = TRUE)) %>%
arrange(avg_dep_delay) %>%
head(2)# A tibble: 2 × 2
hour avg_dep_delay
<dbl> <dbl>
1 5 0.688
2 6 1.64
(3) To compute the total minutes of delay for each destination, we can group the flights by destination and calculate the total arrival and departure delays. And then we can add those two values together to get the total delay for each destination.
flights %>%
group_by(dest) %>%
summarise(total_delay = sum(arr_delay + dep_delay, na.rm = TRUE))# A tibble: 105 × 2
dest total_delay
<chr> <dbl>
1 ABQ 4603
2 ACK 2983
3 ALB 15819
4 ANC 83
5 ATL 399462
6 AUS 45898
7 AVL 4216
8 BDL 10205
9 BGR 9732
10 BHM 12345
# ℹ 95 more rowsflights %>%
group_by(dest) %>%
mutate(total_delay = arr_delay + dep_delay) %>%
mutate(prop_delay = total_delay / sum(total_delay, na.rm = TRUE))# A tibble: 336,776 × 21
# Groups: dest [105]
year month day dep_time sched_dep_time dep_delay arr_time sched_arr_time
<int> <int> <int> <int> <int> <dbl> <int> <int>
1 2013 1 1 517 515 2 830 819
2 2013 1 1 533 529 4 850 830
3 2013 1 1 542 540 2 923 850
4 2013 1 1 544 545 -1 1004 1022
5 2013 1 1 554 600 -6 812 837
6 2013 1 1 554 558 -4 740 728
7 2013 1 1 555 600 -5 913 854
8 2013 1 1 557 600 -3 709 723
9 2013 1 1 557 600 -3 838 846
10 2013 1 1 558 600 -2 753 745
# ℹ 336,766 more rows
# ℹ 13 more variables: arr_delay <dbl>, carrier <chr>, flight <int>,
# tailnum <chr>, origin <chr>, dest <chr>, air_time <dbl>, distance <dbl>,
# hour <dbl>, minute <dbl>, time_hour <dttm>, total_delay <dbl>,
# prop_delay <dbl>(4)
(5) For each plane in each month, we can group the flights data by tailnum and month
flights %>%
group_by(tailnum, month) %>%
summarise(flights = n())# A tibble: 37,988 × 3
# Groups: tailnum [4,044]
tailnum month flights
<chr> <int> <int>
1 D942DN 2 1
2 D942DN 3 2
3 D942DN 7 1
4 N0EGMQ 1 41
5 N0EGMQ 2 28
6 N0EGMQ 3 30
7 N0EGMQ 4 29
8 N0EGMQ 5 13
9 N0EGMQ 6 32
10 N0EGMQ 7 11
# ℹ 37,978 more rowslibrary(agricolae)
iris.aov <- aov(Sepal.Length ~ Species, data = iris)
summary(iris.aov) Df Sum Sq Mean Sq F value Pr(>F)
Species 2 63.21 31.606 119.3 <2e-16 ***
Residuals 147 38.96 0.265
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1LSD.test(iris.aov, "Species", console = TRUE)
Study: iris.aov ~ "Species"
LSD t Test for Sepal.Length
Mean Square Error: 0.2650082
Species, means and individual ( 95 %) CI
Sepal.Length std r LCL UCL Min Max
setosa 5.006 0.3524897 50 4.862126 5.149874 4.3 5.8
versicolor 5.936 0.5161711 50 5.792126 6.079874 4.9 7.0
virginica 6.588 0.6358796 50 6.444126 6.731874 4.9 7.9
Alpha: 0.05 ; DF Error: 147
Critical Value of t: 1.976233
least Significant Difference: 0.2034688
Treatments with the same letter are not significantly different.
Sepal.Length groups
virginica 6.588 a
versicolor 5.936 b
setosa 5.006 cpairwise.t.test(iris$Sepal.Length, iris$Species, p.adjust.method = "bonferroni")
Pairwise comparisons using t tests with pooled SD
data: iris$Sepal.Length and iris$Species
setosa versicolor
versicolor 2.6e-15 -
virginica < 2e-16 8.3e-09
P value adjustment method: bonferroni inflen <- data.frame("HTC"= c(38, 40, 32, 36, 40, 40, 38, 40, 38, 40, 36, 40, 40, 35, 45,
56, 60, 50, 50, 50, 35, 40, 40, 55, 35,
40, 42, 38, 46, 36),
"Source" = c(rep("Control",15),
rep("Dushu",10),
rep("Jinji",5)))
wg_aov1 <- aov(HTC~Source, data = inflen)
summary(wg_aov1) Df Sum Sq Mean Sq F value Pr(>F)
Source 2 450.5 225.23 6.669 0.00443 **
Residuals 27 911.8 33.77
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1summary(LSD.test(wg_aov1, "Source", alpha = 0.01,console = T))
Study: wg_aov1 ~ "Source"
LSD t Test for HTC
Mean Square Error: 33.7716
Source, means and individual ( 99 %) CI
HTC std r LCL UCL Min Max
Control 38.53333 2.996824 15 34.37598 42.69069 32 45
Dushu 47.10000 8.987028 10 42.00830 52.19170 35 60
Jinji 40.40000 3.847077 5 33.19925 47.60075 36 46
Alpha: 0.01 ; DF Error: 27
Critical Value of t: 2.770683
Groups according to probability of means differences and alpha level( 0.01 )
Treatments with the same letter are not significantly different.
HTC groups
Dushu 47.10000 a
Jinji 40.40000 ab
Control 38.53333 b Length Class Mode
statistics 4 data.frame list
parameters 5 data.frame list
means 10 data.frame list
comparison 0 -none- NULL
groups 2 data.frame listinflen_pt <- pairwise.t.test(inflen$HTC, inflen$Source, pool.sd = FALSE,var.equal = TRUE, p.adj = "bonferroni")
inflen_pt
Pairwise comparisons using t tests with non-pooled SD
data: inflen$HTC and inflen$Source
Control Dushu
Dushu 0.0066 -
Jinji 0.8227 0.4191
P value adjustment method: bonferroni inflen_pt$p.value < 0.01 Control Dushu
Dushu TRUE NA
Jinji FALSE FALSEWilcoxon Rank-Sum test: Used to compare whether the medians of two independent groups are equal. It is suitable for situations where the sample does not follow a normal distribution or where the variances are unequal.
Wilcoxon Signed-Rank test: Used to compare whether the medians of two related groups are equal. It is suitable for situations where the sample does not follow a normal distribution or where the variances are unequal.
Kruskal-Wallis test: Used to compare whether the medians of three or more independent groups are equal. It is suitable for situations where the sample does not follow a normal distribution or where the variances are unequal.
Friedman test: Used to compare whether the medians of three or more related groups are equal. It is suitable for situations where the sample does not follow a normal distribution or where the variances are unequal.
dtf <- read.csv('data/tce.csv')
wilcox.test(dtf$TCE.mg.per.L[dtf$Period == 'Before'],
dtf$TCE.mg.per.L[dtf$Period == 'After'],
paired = TRUE, conf.int = TRUE,
correct = FALSE)
Wilcoxon signed rank exact test
data: dtf$TCE.mg.per.L[dtf$Period == "Before"] and dtf$TCE.mg.per.L[dtf$Period == "After"]
V = 55, p-value = 0.001953
alternative hypothesis: true location shift is not equal to 0
95 percent confidence interval:
6.8650 28.5715
sample estimates:
(pseudo)median
18.78 kruskal.test(Sepal.Length ~ Species, data = iris)
Kruskal-Wallis rank sum test
data: Sepal.Length by Species
Kruskal-Wallis chi-squared = 96.937, df = 2, p-value < 2.2e-16boxplot(Sepal.Length ~ Species,
data = iris,
horizontal = TRUE,
notch = TRUE, las = 1)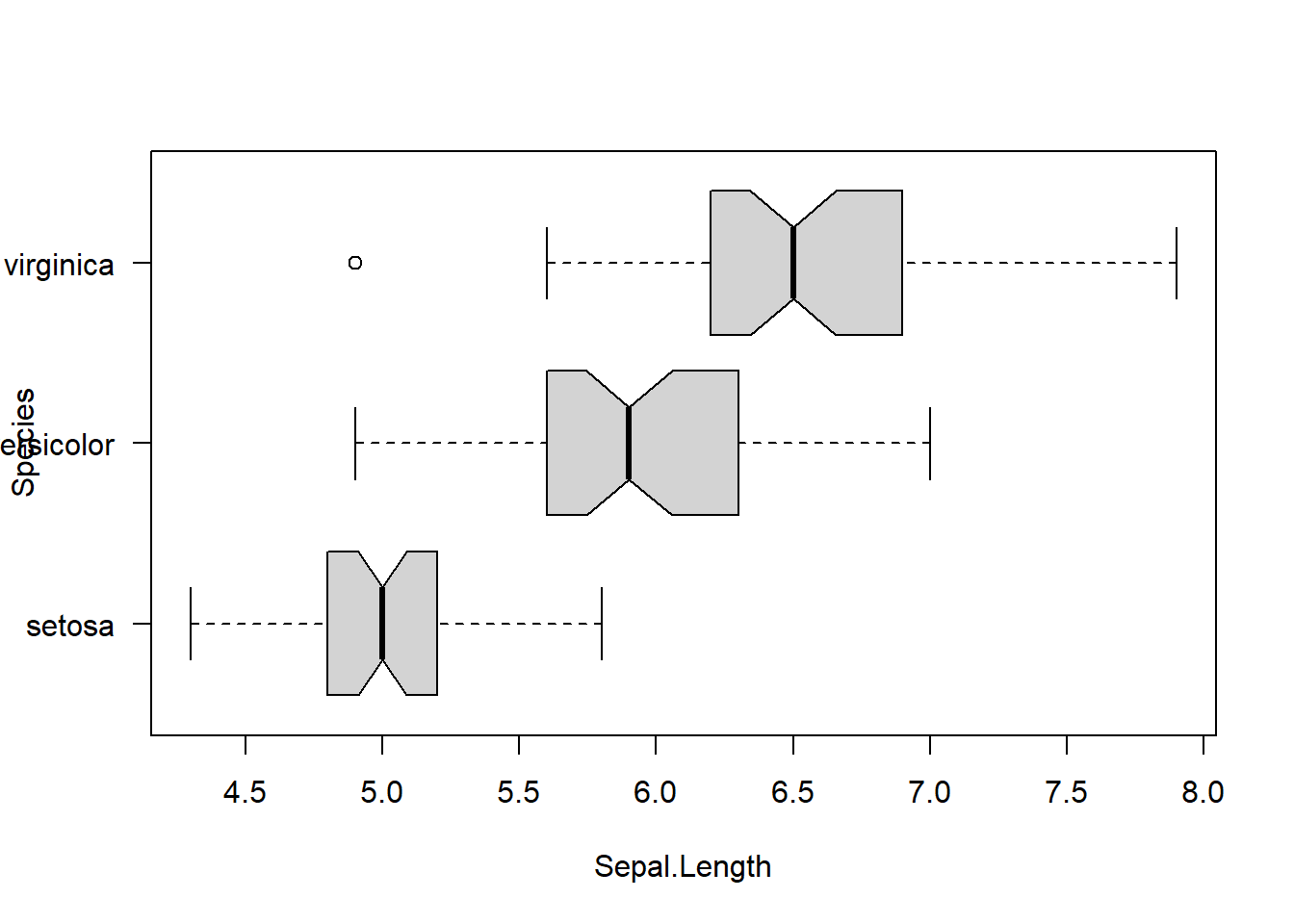
# Step 1: Visualization
dtf <- airquality[, -6]
dtf <- na.omit(dtf)
dtf_cor <- cor(dtf)
GGally::ggpairs(dtf)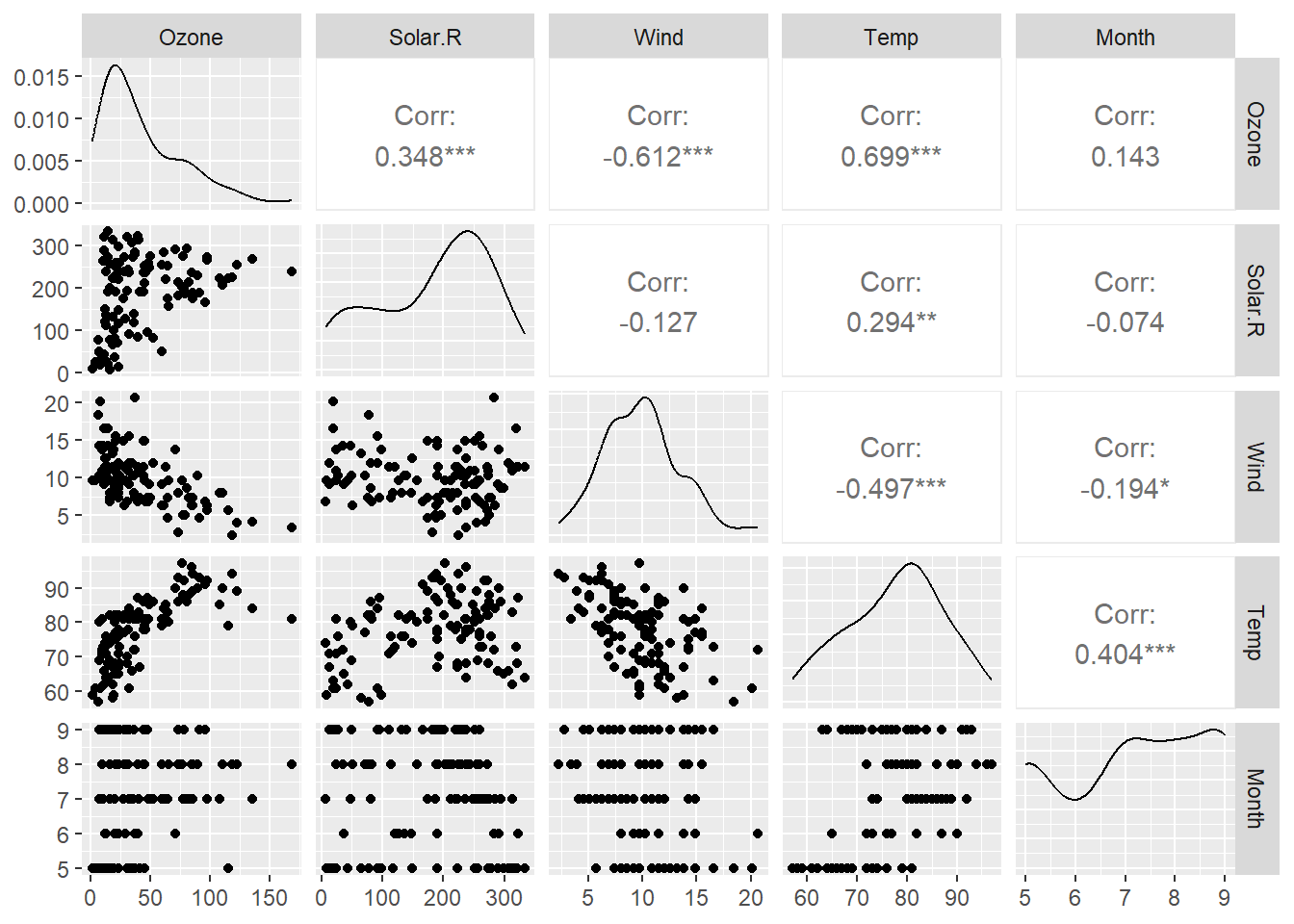
pairs(dtf)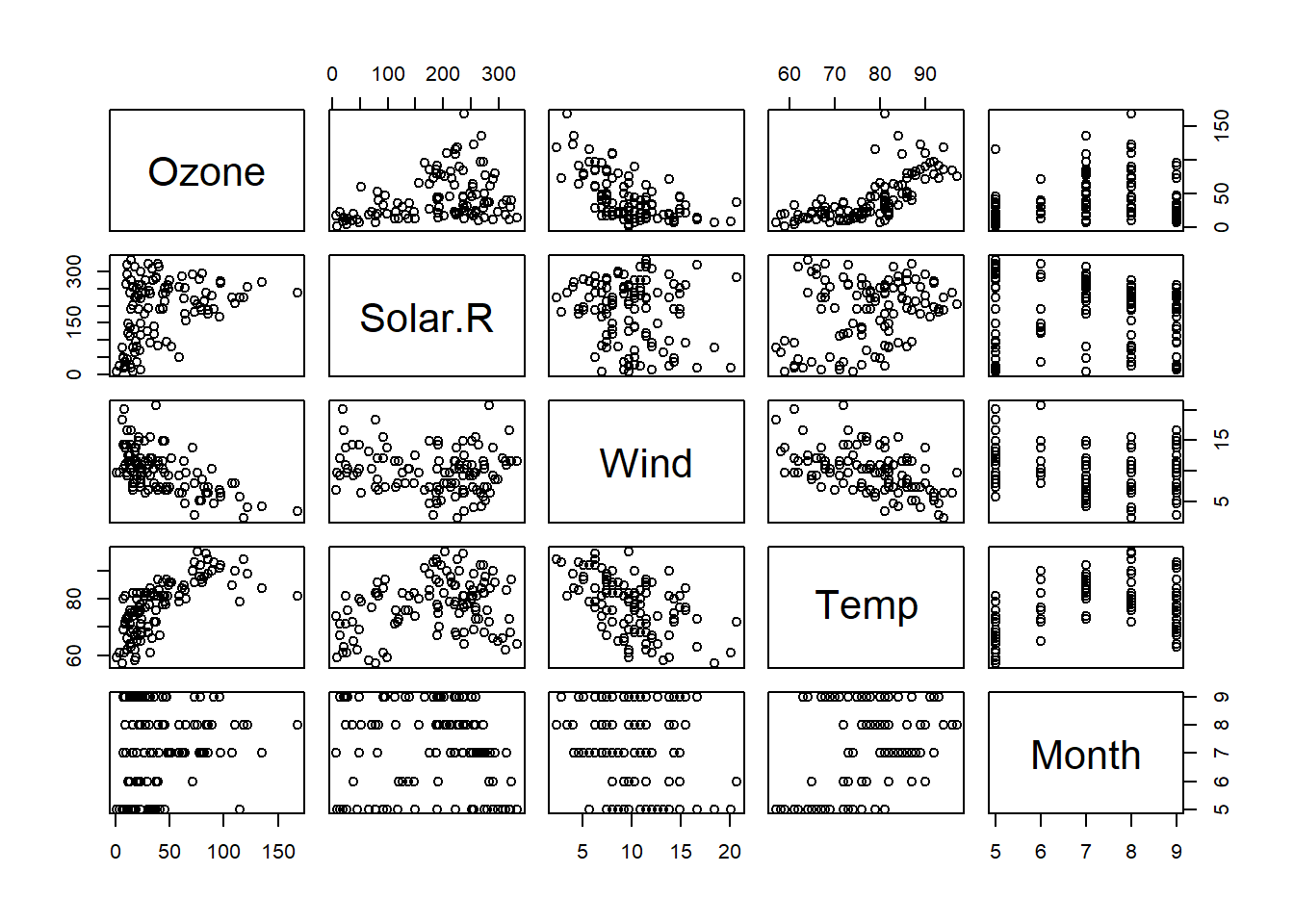
corrplot::corrplot(dtf_cor,
order = 'AOE',
type = "upper",
method = "number")
corrplot::corrplot(dtf_cor,
order = "AOE",
type = "lower",
method = "ell",
diag = FALSE,
tl.pos = "l",
cl.pos = "n",
add = TRUE)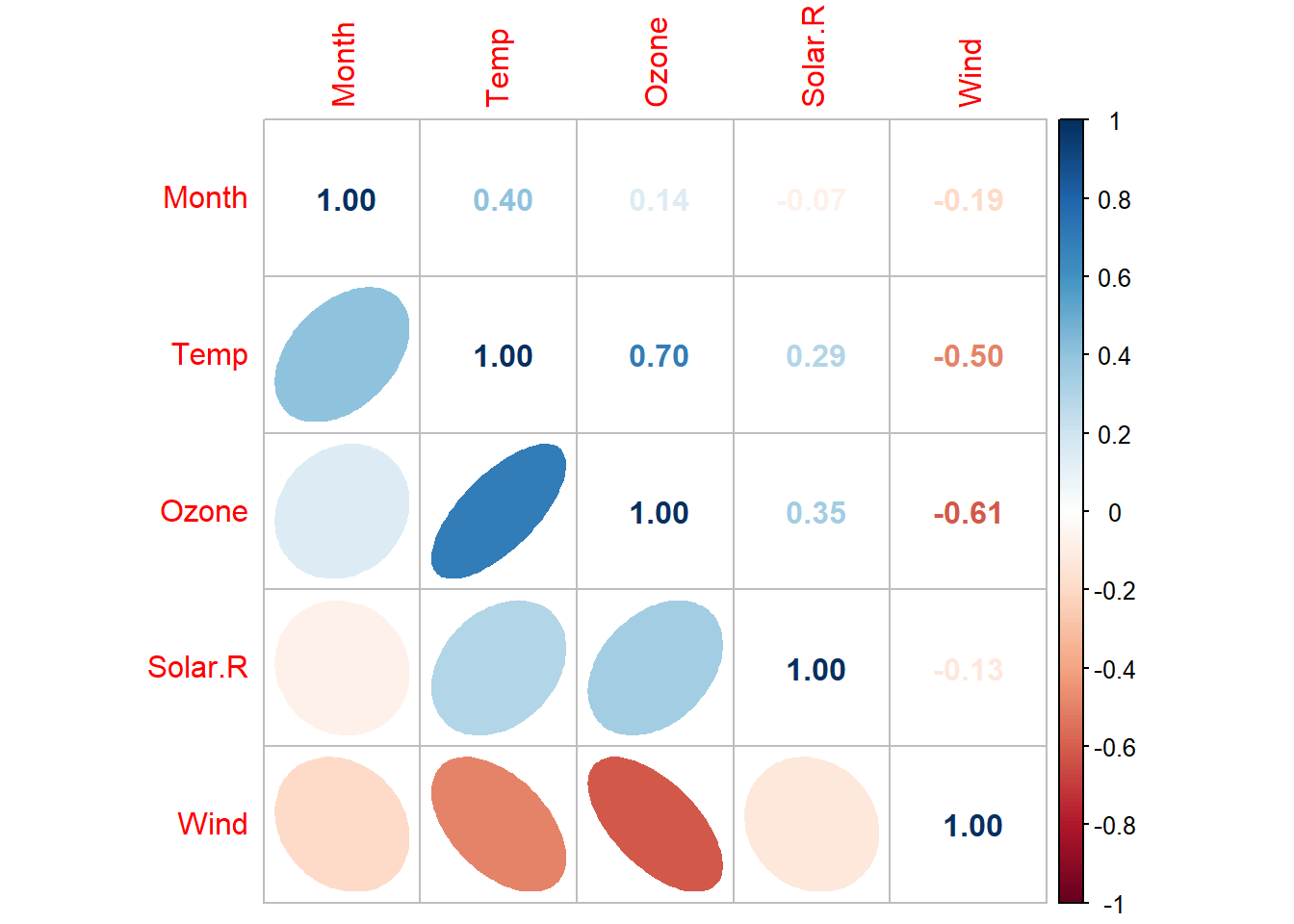
# Step 2: Maximal model
ozone_concentration_lm <- lm(Ozone ~ ., data = dtf)
summary(ozone_concentration_lm)
Call:
lm(formula = Ozone ~ ., data = dtf)
Residuals:
Min 1Q Median 3Q Max
-35.870 -13.968 -2.671 9.553 97.918
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -58.05384 22.97114 -2.527 0.0130 *
Solar.R 0.04960 0.02346 2.114 0.0368 *
Wind -3.31651 0.64579 -5.136 1.29e-06 ***
Temp 1.87087 0.27363 6.837 5.34e-10 ***
Month -2.99163 1.51592 -1.973 0.0510 .
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 20.9 on 106 degrees of freedom
Multiple R-squared: 0.6199, Adjusted R-squared: 0.6055
F-statistic: 43.21 on 4 and 106 DF, p-value: < 2.2e-16confint(ozone_concentration_lm) 2.5 % 97.5 %
(Intercept) -1.035964e+02 -12.51131722
Solar.R 3.088529e-03 0.09610512
Wind -4.596849e+00 -2.03616955
Temp 1.328372e+00 2.41337586
Month -5.997092e+00 0.01383629anova(ozone_concentration_lm)Analysis of Variance Table
Response: Ozone
Df Sum Sq Mean Sq F value Pr(>F)
Solar.R 1 14780 14780 33.8357 6.427e-08 ***
Wind 1 39969 39969 91.5037 5.327e-16 ***
Temp 1 19050 19050 43.6117 1.639e-09 ***
Month 1 1701 1701 3.8946 0.05104 .
Residuals 106 46302 437
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1# Step 3: Check the Multicollinearity
faraway::vif(dtf[, -1]) Solar.R Wind Temp Month
1.151409 1.329309 1.712455 1.256371 # Step 4: simplify the model using Backward selection
get_p <- function(model){
smry2 <- data.frame(summary(model)$coefficients)
smry2[order(-smry2$Pr...t..), ]
}
get_p(ozone_concentration_lm) Estimate Std..Error t.value Pr...t..
Month -2.99162786 1.51592267 -1.973470 5.104492e-02
Solar.R 0.04959683 0.02345827 2.114258 3.683836e-02
(Intercept) -58.05383883 22.97114118 -2.527251 1.297198e-02
Wind -3.31650940 0.64578918 -5.135591 1.286145e-06
Temp 1.87087379 0.27363201 6.837189 5.337230e-10lm2 <- update(ozone_concentration_lm,.~.-Month)
get_p(lm2) Estimate Std..Error t.value Pr...t..
Solar.R 0.05982059 0.02318647 2.579979 1.123664e-02
(Intercept) -64.34207893 23.05472435 -2.790841 6.226638e-03
Wind -3.33359131 0.65440710 -5.094063 1.515934e-06
Temp 1.65209291 0.25352979 6.516366 2.423506e-09lm3 <- step(ozone_concentration_lm, direction = "both")Start: AIC=679.71
Ozone ~ Solar.R + Wind + Temp + Month
Df Sum of Sq RSS AIC
<none> 46302 679.71
- Month 1 1701.2 48003 681.71
- Solar.R 1 1952.6 48254 682.29
- Wind 1 11520.5 57822 702.37
- Temp 1 20419.5 66721 718.26# Step 5: report the results
summary(lm2)
Call:
lm(formula = Ozone ~ Solar.R + Wind + Temp, data = dtf)
Residuals:
Min 1Q Median 3Q Max
-40.485 -14.219 -3.551 10.097 95.619
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -64.34208 23.05472 -2.791 0.00623 **
Solar.R 0.05982 0.02319 2.580 0.01124 *
Wind -3.33359 0.65441 -5.094 1.52e-06 ***
Temp 1.65209 0.25353 6.516 2.42e-09 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 21.18 on 107 degrees of freedom
Multiple R-squared: 0.6059, Adjusted R-squared: 0.5948
F-statistic: 54.83 on 3 and 107 DF, p-value: < 2.2e-16stargazer::stargazer(lm2, type = 'text')
===============================================
Dependent variable:
---------------------------
Ozone
-----------------------------------------------
Solar.R 0.060**
(0.023)
Wind -3.334***
(0.654)
Temp 1.652***
(0.254)
Constant -64.342***
(23.055)
-----------------------------------------------
Observations 111
R2 0.606
Adjusted R2 0.595
Residual Std. Error 21.181 (df = 107)
F Statistic 54.834*** (df = 3; 107)
===============================================
Note: *p<0.1; **p<0.05; ***p<0.01dtf <- read.csv("data/heart.data.csv")
dtf <- dtf[, -1]
dtf <- na.omit(dtf)
dtf_cor <- cor(dtf)
GGally::ggpairs(dtf)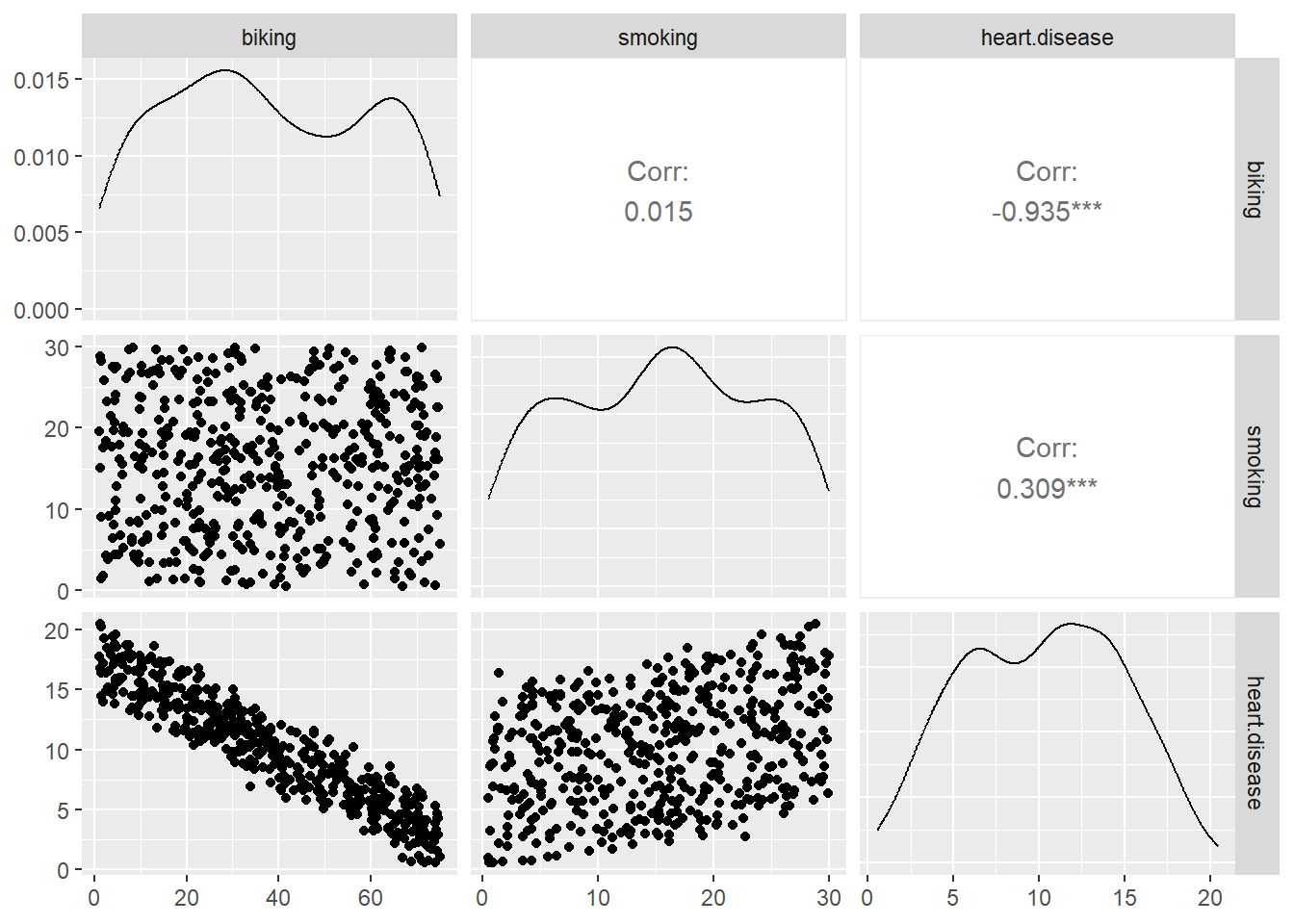
corrplot::corrplot(dtf_cor,
order = 'AOE',
type = "upper",
method = "number")
corrplot::corrplot(dtf_cor,
order = "AOE",
type = "lower",
method = "ell",
diag = FALSE,
tl.pos = "l",
cl.pos = "n",
add = TRUE)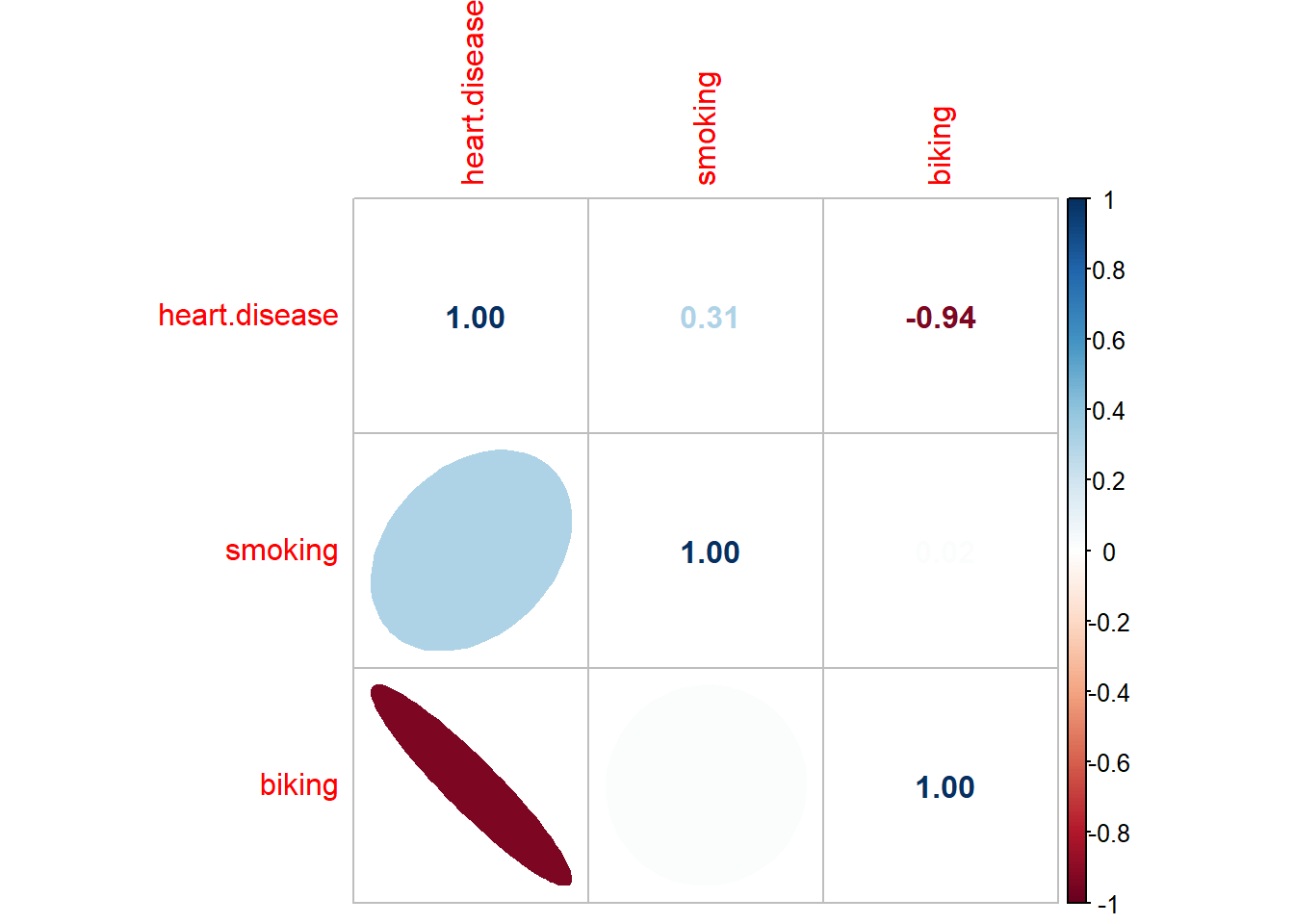
heart_disease_lm <- lm(heart.disease ~ ., data = dtf)
summary(heart_disease_lm)
Call:
lm(formula = heart.disease ~ ., data = dtf)
Residuals:
Min 1Q Median 3Q Max
-2.1789 -0.4463 0.0362 0.4422 1.9331
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 14.984658 0.080137 186.99 <2e-16 ***
biking -0.200133 0.001366 -146.53 <2e-16 ***
smoking 0.178334 0.003539 50.39 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.654 on 495 degrees of freedom
Multiple R-squared: 0.9796, Adjusted R-squared: 0.9795
F-statistic: 1.19e+04 on 2 and 495 DF, p-value: < 2.2e-16confint(heart_disease_lm) 2.5 % 97.5 %
(Intercept) 14.8272075 15.1421084
biking -0.2028166 -0.1974495
smoking 0.1713800 0.1852878anova(heart_disease_lm)Analysis of Variance Table
Response: heart.disease
Df Sum Sq Mean Sq F value Pr(>F)
biking 1 9090.6 9090.6 21251.7 < 2.2e-16 ***
smoking 1 1086.0 1086.0 2538.8 < 2.2e-16 ***
Residuals 495 211.7 0.4
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1faraway::vif(dtf[, 1:2]) biking smoking
1.000229 1.000229 get_p <- function(model){
smry2 <- data.frame(summary(model)$coefficients)
smry2[order(-smry2$Pr...t..), ]
}
get_p(heart_disease_lm) Estimate Std..Error t.value Pr...t..
smoking 0.1783339 0.003539307 50.38667 5.192235e-197
(Intercept) 14.9846580 0.080136914 186.98821 0.000000e+00
biking -0.2001331 0.001365858 -146.52547 0.000000e+00stargazer::stargazer(heart_disease_lm, type = 'text')
===============================================
Dependent variable:
---------------------------
heart.disease
-----------------------------------------------
biking -0.200***
(0.001)
smoking 0.178***
(0.004)
Constant 14.985***
(0.080)
-----------------------------------------------
Observations 498
R2 0.980
Adjusted R2 0.980
Residual Std. Error 0.654 (df = 495)
F Statistic 11,895.240*** (df = 2; 495)
===============================================
Note: *p<0.1; **p<0.05; ***p<0.01To be continue…
A scientist studies the effect of seizure drugs on the number of seizures during the first eight weeks of treatment. The dataset is available in the robust package:
Carry out a Poisson regression of the number of seizures after treatment (sumY) as the dependent variable, and the treatment conditions (Trt), Age, and the number of seizures before treatment (Base) as the independent variables.
data("breslow.dat", package = 'robust')
View(breslow.dat)
fit.breslow <- glm(sumY ~ Trt + Age + Base, data = breslow.dat, family = poisson())
summary(fit.breslow)
Call:
glm(formula = sumY ~ Trt + Age + Base, family = poisson(), data = breslow.dat)
Deviance Residuals:
Min 1Q Median 3Q Max
-6.0569 -2.0433 -0.9397 0.7929 11.0061
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 1.9488259 0.1356191 14.370 < 2e-16 ***
Trtprogabide -0.1527009 0.0478051 -3.194 0.0014 **
Age 0.0227401 0.0040240 5.651 1.59e-08 ***
Base 0.0226517 0.0005093 44.476 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 2122.73 on 58 degrees of freedom
Residual deviance: 559.44 on 55 degrees of freedom
AIC: 850.71
Number of Fisher Scoring iterations: 5exp(coef(fit.breslow)) (Intercept) Trtprogabide Age Base
7.0204403 0.8583864 1.0230007 1.0229102 stargazer::stargazer(fit.breslow, type = 'text')
=============================================
Dependent variable:
---------------------------
sumY
---------------------------------------------
Trtprogabide -0.153***
(0.048)
Age 0.023***
(0.004)
Base 0.023***
(0.001)
Constant 1.949***
(0.136)
---------------------------------------------
Observations 59
Log Likelihood -421.354
Akaike Inf. Crit. 850.707
=============================================
Note: *p<0.1; **p<0.05; ***p<0.01equatiomatic::extract_eq(fit.breslow, use_coefs = TRUE)\[ \log ({ \widehat{E( \operatorname{sumY} )} }) = 1.95 - 0.15(\operatorname{Trt}_{\operatorname{progabide}}) + 0.02(\operatorname{Age}) + 0.02(\operatorname{Base}) \]
fit.breslow.od <- glm(sumY ~ Trt + Age + Base, data = breslow.dat, family = quasipoisson())
summary(fit.breslow.od)
Call:
glm(formula = sumY ~ Trt + Age + Base, family = quasipoisson(),
data = breslow.dat)
Deviance Residuals:
Min 1Q Median 3Q Max
-6.0569 -2.0433 -0.9397 0.7929 11.0061
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.948826 0.465091 4.190 0.000102 ***
Trtprogabide -0.152701 0.163943 -0.931 0.355702
Age 0.022740 0.013800 1.648 0.105085
Base 0.022652 0.001747 12.969 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for quasipoisson family taken to be 11.76075)
Null deviance: 2122.73 on 58 degrees of freedom
Residual deviance: 559.44 on 55 degrees of freedom
AIC: NA
Number of Fisher Scoring iterations: 5exp(coef(fit.breslow.od)) (Intercept) Trtprogabide Age Base
7.0204403 0.8583864 1.0230007 1.0229102 stargazer::stargazer(fit.breslow.od, type = 'text')
========================================
Dependent variable:
---------------------------
sumY
----------------------------------------
Trtprogabide -0.153
(0.164)
Age 0.023
(0.014)
Base 0.023***
(0.002)
Constant 1.949***
(0.465)
----------------------------------------
Observations 59
========================================
Note: *p<0.1; **p<0.05; ***p<0.01equatiomatic::extract_eq(fit.breslow.od, use_coefs = TRUE)\[ \log ({ \widehat{E( \operatorname{sumY} )} }) = 1.95 - 0.15(\operatorname{Trt}_{\operatorname{progabide}}) + 0.02(\operatorname{Age}) + 0.02(\operatorname{Base}) \]
R version 4.2.3 (2023-03-15 ucrt)
Platform: x86_64-w64-mingw32/x64 (64-bit)
Running under: Windows 10 x64 (build 19044)
Matrix products: default
locale:
[1] LC_COLLATE=Chinese (Simplified)_China.utf8
[2] LC_CTYPE=Chinese (Simplified)_China.utf8
[3] LC_MONETARY=Chinese (Simplified)_China.utf8
[4] LC_NUMERIC=C
[5] LC_TIME=English_United States.1252
attached base packages:
[1] stats graphics grDevices utils datasets methods base
other attached packages:
[1] agricolae_1.3-5 nycflights13_1.0.2 lubridate_1.9.2 forcats_1.0.0
[5] stringr_1.5.0 purrr_1.0.1 readr_2.1.4 tidyr_1.3.0
[9] tibble_3.2.1 ggplot2_3.4.2 tidyverse_2.0.0 openair_2.16-0
[13] dplyr_1.1.0 latex2exp_0.9.6
loaded via a namespace (and not attached):
[1] nlme_3.1-162 RColorBrewer_1.1-3 backports_1.4.1
[4] tools_4.2.3 utf8_1.2.3 R6_2.5.1
[7] AlgDesign_1.2.1 mgcv_1.8-42 questionr_0.7.8
[10] colorspace_2.1-0 withr_2.5.0 tidyselect_1.2.0
[13] GGally_2.1.2 klaR_1.7-2 compiler_4.2.3
[16] cli_3.6.1 labeling_0.4.2 equatiomatic_0.3.1
[19] scales_1.2.1 hexbin_1.28.3 digest_0.6.31
[22] minqa_1.2.5 rmarkdown_2.21 jpeg_0.1-10
[25] pkgconfig_2.0.3 htmltools_0.5.4 lme4_1.1-31
[28] labelled_2.11.0 fastmap_1.1.0 highr_0.10
[31] maps_3.4.1 htmlwidgets_1.6.2 rlang_1.1.0
[34] rstudioapi_0.14 shiny_1.7.4 generics_0.1.3
[37] farver_2.1.1 combinat_0.0-8 jsonlite_1.8.4
[40] magrittr_2.0.3 interp_1.1-4 Matrix_1.5-3
[43] Rcpp_1.0.10 munsell_0.5.0 fansi_1.0.3
[46] lifecycle_1.0.3 stringi_1.7.12 yaml_2.3.7
[49] MASS_7.3-58.2 plyr_1.8.8 grid_4.2.3
[52] promises_1.2.0.1 miniUI_0.1.1.1 deldir_1.0-6
[55] lattice_0.20-45 stargazer_5.2.3 haven_2.5.2
[58] splines_4.2.3 mapproj_1.2.11 hms_1.1.3
[61] knitr_1.42 pillar_1.9.0 boot_1.3-28.1
[64] glue_1.6.2 evaluate_0.20 latticeExtra_0.6-30
[67] nloptr_2.0.3 png_0.1-8 vctrs_0.6.2
[70] tzdb_0.3.0 httpuv_1.6.9 gtable_0.3.3
[73] reshape_0.8.9 xfun_0.37 mime_0.12
[76] broom_1.0.4 xtable_1.8-4 later_1.3.0
[79] faraway_1.0.8 cluster_2.1.4 corrplot_0.92
[82] timechange_0.2.0 ellipsis_0.3.2